Definizione e formule del triangolo in tutte le sue tipologie
Il triangolo è un poligono formato da tre lati e tre angoli e può avere diverse forme perché diverse sono i gradi dei suoi angoli. Ma le diverse forme creano altrettante figure geometriche che sono sempre dei triangoli ma con definizioni diverse perché con angoli diversi. I lati rimangono sempre tre ma a seconda del grado degli angoli questi formano figure diverse che vengono trattati in questo articolo. Qui ci occuperemo di tutte le formule dirette e indirette di ogni singola figura, presentando un formulario che racchiude tutte le formule possibili. I triangoli che tratteremo sono rettangolo, equilatero, isoscele, scaleno. Adesso li analizziamo uno per volta in modo da non fare confusione.
Il Triangolo
leggi pure : fare screenshot su android
Ora man mano che trattiamo ogni singola figura geometrica sopra elencata, vi accorgerete come è semplicissimo capire le formule senza bisogno di impararle a memoria. Basterà capire i meccanismi e tutto sarà semplice. Esiste un modo semplice per formare un triangolo rettangolo preciso usando solo il metro. Si basa sul teorema di Pitagora e consiste in questo. Se formiamo un triangolo aventi i due lati uno di 60 cm; l’altro di 80 cm l’ipotenusa sarà di 100 cm ed il triangolo rettangolo sarà preciso. Questo perché se moltiplichiamo il primo lato per se stesso, abbiamo 3600; moltiplichiamo adesso il secondo lato per se stesso e abbiamo 6400; la somma dei due lati è uguale a 10000 che è uguale a l’ipotenusa moltiplicata per se stessa; e cioè 100 x 100 uguale a 10000.
* Il triangolo rettangolo
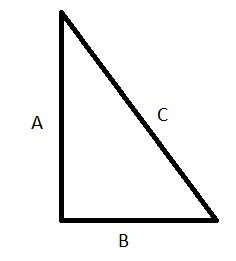
Il triangolo rettangolo così definito perché uno dei suoi angoli è un angolo retto da 90° i suoi lati sono A cateto maggiore B cateto minore e C è l’ ipotenusa. Se osserviamo attentamente la figura è l’esatta metà di un rettangolo; quindi molte formule potremmo recuperarle dal rettangolo ricordandoci che poi bisognerebbe dividere per 2 nel caso dell’area. Ma adesso osserviamo quali sono le formule per questa figura.
Fai un regalo, regala buoni acquisto Amazon
| Formule triangolo rettangolo | ||||
| Perimetro | lato A + lato B + lato C | |||
| Lato A | Perimetro – lato b – lato C | |||
| Lato B | Perimetro – lato A – lato C | |||
| Lato C | Perimetro – lato A – lato B | |||
| Area | lato A x lato B : 2 | |||
| Lato B da area | Area x 2 : lato C | |||
| Lato A da area | Area x 2 : lato B | Teorema di Pitagora | ||
| Lato A | √ lato B² – lato C² | |||
| Lato B | √ lato A² – lato C² | |||
| Ipotenusa | √ lato A² + lato B² | |||
Se questo articolo ti è stato utile condividilo
* Triangolo equilatero
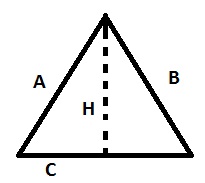
Il triangolo equilatero è denominato così perché è una figura geometrica che è formata da tre lati tutti uguali come uguali sono i suoi tre angoli. Quindi possiamo definirlo anche equiangolo perché oltre ai lati ha anche gli angoli congrui. Possiamo anche dire che tracciando l’altezza formiamo 2 triangoli rettangoli questo ci sarà utile nelle formule.
| Formule triangolo equilatero | ||||
| Perimetro | lato x 3 | |||
| Lato da perimetro | Perimetro : 3 | |||
| Area | Lato C x H Altezza | Teorema di Pitagora | ||
| Lato A | √ Altezza H² + (lato C² : 2) | |||
| Lato B | √ Altezza H² + (lato C² : 2) | |||
| Altezza H | √ lato A o B² – (lato C² : 2) | |||
* Triangolo isoscele
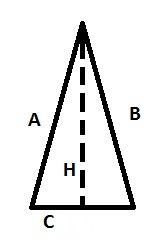
Il triangolo isoscele si riconosce subito per via che ha 2 lati e 2 angoli uguali, e questa è la sua caratteristica. Quindi non ci si può sbagliare, basta una occhiata e si capisce subito se è un triangolo isoscele. Adesso vediamo quali sono le sue formule per ottenere area perimetro ecc.
| Formule triangolo isoscele | ||||
| Perimetro | lato A + lato B + lato C | |||
| Lato A da perimetro | Perimetro – lato C : 2 | |||
| Lato B da perimetro | Perimetro – lato C : 2 | |||
| Lato C da perimetro | Perimetro – lato A o B x 2 | |||
| Area | C x H : 2 | |||
| Altezza H da area | Area x 2 : lato C | |||
| Lato C da area | Area x 2 : H Altezza | Teorema di Pitagora | ||
| Lato A | √ (lato C² : 2) + H² | |||
| Lato B | √ lato H² + (lato C² : 2) | |||
| H Altezza | √ lato A² – (lato C² : 2) | |||
| C Base | √ lato A² – H² | |||
* Triangolo scaleno
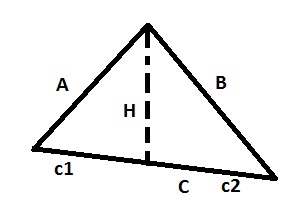
Il triangolo scaleno è una figura geometrica avente tutti e tre i lati di misura diversa. Anche gli angoli sono di gradi diversi e di conseguenza in questa figura possono esserci tre altezze diverse. Noi per non elencare una infinità di formule ne segneremo una che serve come indicazione. Questo perché sapendo questa, le formule sono le stesse dovete solo cambiare i dati. Ogni altezza parte da un vertice quindi può cadere sul lato A B o C; basta tener presente questo e si ricavano gli altri lati per usare il teorema di Pitagora.
| Formule triangolo Scaleno | ||||
| Perimetro | lato A + lato B + lato C | |||
| Lato A | Perimetro – lato b – lato C | |||
| Lato B | Perimetro – lato A – lato C | |||
| Lato C | Perimetro – lato A – lato B | |||
| Area | Lato C1 x Altezza H : 2 | |||
| Area 2 | C2 x Altezza H : 2 | |||
| Teorema di Pitagora | ||||
| Lato A | √ Altezza H² + lato C1² | |||
| Lato B | √ Altezza H² + lato C2² | |||
| Altezza H | √ lato A o B² – lato B² | |||
| Lato C1 o C2 | √ Altezza H² – lato A o B² | |||
Con queste schede abbiamo trattato parte delle formule che riguardano queste figure geometriche; perché sono quelle che vanno per la maggiore. Trattare l’argomento in maniera più completa è utile solamente a certi livelli; ma ci vorrebbe più spazio per ogni singola figura per essere chiari e non fare confusione. In questi casi essere chiari e generare meno confusione è molto importante; perché chi cerca con una certa fretta potrebbe impallarsi.
